பஞ்சரத்தினத்தின் வடிவியற்கட்டம்
(Pancharatnam geometric phase)
தளவிளைவுற்ற ஒளியும் நவீன குவாண்டத் தொடர்பு அறிவியலும்
இரா. நாகேஸ்வரன்_
eswar.quanta @ gmail.com
- பஞ்சரத்தினம் யார்?
சிவராமகிருஷ்ண பஞ்சரத்தினம், 1934 ஆம் ஆண்டு கல்கத்தாவில் பிறந்த ஒரு இயற்பியலாளர் ஆவார், அடிப்படையில் தமிழ் குடும்பமான அவர்கள், பஞ்சரத்தினத்தின் தந்தையின் வேலை நிமித்தம் வங்காளத்தில் வாழ்ந்தனர். இவர் சர் சி. வி. இராமனின் தங்கையின் மகனும் ஆவார். மிகச்சிறிய வயதில் சில ஒளியியற் சோதனைகளைச் செய்து அதில் மிக முக்கியமான விளைவுகளைக் கண்டறிந்தவர். இவரின் தொடக்க கால ஆய்வுகள் இராமனின் மேற்பார்வையிலேயே நடந்தன. பெரிதாக அறியப்படாத இந்திய அறிவியலாளர்களில் இவரும் ஒருவர்.
சர். சி. வி. இராமன் பஞ்சரத்தினத்தின் திறனை நன்கு உணர்ந்திருந்தார், அவர் ஜவஹர்லால் நேருவிடம் ஒரு முறை பஞ்சரத்தினத்தைச் சுட்டிக்காட்டி, அந்த இளைஞன் இந்தியாவிற்கு மற்றுமொரு நோபல் பரிசைக் கொணர்வான் எனக் கூறினாராம். இப்படித் திறமையுடன் வலம் வந்தவர், ஆக்ஸ்போர்டு பல்கலைக்கழகத்தில் ஆய்வு செய்ய சென்று இருந்த போது, தனது 35-வது வயதில், 1969 ல் நோய்வாய்ப்பட்டு இறந்தார். எனினும் அவர் தன் குறுகிய வாழ்நாளில் கண்டுபிடித்தவை, இயற்பியலிலும், கணினித் துறையிலும் மிக முக்கியமானதாகக் கருதப்படுகிறது.
அவரால், 1950வாக்கில் கண்டறியப்பட்டவை, அக்காலத்தில் சிலத் தாக்கங்களை உண்டுபண்ணியிருந்தாலும், 1984 ஆம் ஆண்டு மைக்கேல் பெரி (Michael V Berry) என்பாரால் கண்டறியப்பட்ட பெரியின் வடிவியற்கட்டம் (Berry’s geometric phase) வந்தப் பின்னரே, பரந்த இயற்பியல் ஆய்வுலகத்துக்கு பஞ்சரத்தினத்தின் ஆய்வினை, இராமன் ஆய்வுக்கழகத்தைச் சார்ந்த பேராசிரியர் இராஜாராம் நித்யானந்தாவும், இந்திய அறிவியற்கழகப் பேராசிரியரும் பஞ்சரத்தினத்தின் அண்ணனுமான, இராமசேஷனும் அறியச் செய்தனர். ஏறத்தாழ 60 வருடங்கள் ஆன நிலையில், அப்பொழுதுக் கண்டறியப்பட்ட விசயம் எப்படி நவீனக் கணினி மற்றும் தொடர்பியல் கோட்பாட்டை மாற்றி அமைக்க எத்தனிக்கிறது என்பதைச் சுருக்கமாகக் காண்போம்.
படம்: (Courtesy: Resonance, (April 2013)) புகழ்பெற்ற சகோதர இயற்பியலாளர்கள்: பஞ்சரத்தினம், அவரின் அண்ணன்கள் இராமசேஷன் (படிகவியல், பொருண்ம அறிவியல்) மற்றும் சந்திரசேகர் (நீர்மப் படிகவியல்)
- தளவிளைவும் படிகவியலும்
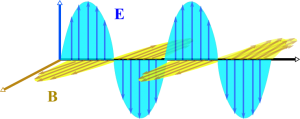
ஒளியானது, பொதுவாக மின்காந்தப் புலங்களைக் கொண்ட அலைகளால் ஆனது, அலைகள் எனக் கூறும் பொழுது, அவை மாறும் தன்மை கொண்டவையென நம்மால் உணரமுடிகிறது, அவ்வாறு ஏற்படும் மாற்றமானது, நொடிக்கு ஏறத்தாழ 10^15 முறை அலைவுறும். அவை குறுக்கலைகளாகப் பரவும், அதாவது, ஒளி பரவும் திசைக்கு செங்குத்தாக புலங்களின் அதிர்வுகள் இருக்கும். அவ்வாறு பரவும் போது, பற்பல கோணங்களில் ஒளிப் பயணிக்கும் திசைக்கு செங்குத்தாக மின்புலத்தின் அதிர்வுகளும் இருக்கும்! எடுத்துக்காட்டாக, இயற்கையில் கிடைக்கும் சூரிய ஒளியானது, பல தளங்களில் அதிர்வுறும் ஒளியாகும். இவ்வாறான தளவிளைவுறா ஒளியை, ஒரு தளத்தில் மட்டும் அதிர்வுறச் செய்யும் போது, நமக்கு தளவிளைவுக்கு உட்படுத்தப்பட்ட ஒளியாகக் கிடைக்கும்.
மேலும் ஒளிப் புகுந்து வரும் ஊடகத்தைப் பொறுத்து, வட்டவடிவமும் நீள்வட்டவடிவத் தளவிளைவாக்கமும் கொணரலாம். அவை, அவ்வூடகத்தின் ஒளியியல் பண்புகளைப் பொறுத்து அமைவன. இரட்டை ஒளிவிலகல் திறன் (birefringence) கொண்டப் படிகம் ஒன்றின் வழியாக, தளவிளைவுறா ஒளியை அனுப்பும் பொழுது, இரண்டாகப் பிரிக்கப்படுகிறது, படிகத்திலிருந்து வெளிவரும் ஒளிக்கதிர்களில், ஒன்று படிகத்தைச் சுழற்றினாலும் ஒளி வரும் திசையிலேயே இருக்கும், மற்றொருக் கதிரானது, படிகத்தைச் சுழற்றும் பொழுது, வெளிவரும் ஒளிக்கதிரின் திசையும் மாறி படிகத்துடன் சேர்ந்து சுழலும். இதற்குக் காரணம், படிகத்தில் விழும் ஒளியானது, பல்வேறு நிலைகளில் படிகத்தில் விலக்கப்பட்டு, வெவ்வேறு திசையில் பயணிக்கும், அவ்வாறு செல்லும் பொழுது, படிகத்தின் அணுக்களின் அமைப்புக்கு ஏற்ப, வெவ்வேறு திசையில் வெவ்வேறு திசைவேகத்தில் செல்லும், இதனால், இம்மாதிரியான இரட்டை ஒளிவிலகல் உண்டாகிறது,
மேலும், இவ்வாறு ஒளிக் கதிர் படிக மூலக்கூறுகளோடு ஊடாடும் பொழுது, தளவிளைவை அக்கதிர்களில் உண்டாக்குகிறது. இவ்வாறு வரும் கதிர்கள், டூர்மலைன் போன்றப் படிகங்களில், வெவ்வேறு தளவிளைவாக்கிய ஒளிக்கற்றைகளாகவும் வெளியேறும்.
- தொலைக்காட்சியின் அலைவாங்கி உதாரணம்
தளவிளைவாக்கப்பட்ட அலைகளின் பண்புகளை, 1980, 1990களில் தொலைக்காட்சிகளுடன் இணைக்கப்பட்ட, ஈய அலைவாங்கிகளைக் (Antenna) நாம் பயன்படுத்தியவிதத்தில் இருந்துப் புரிந்து கொள்ளலாம். தொலைக்காட்சி நிகழ்வுகள் பண்பலையாக்கப்பட்டு, மின்காந்த அலைகளாக அனுப்பப்படும் பொழுது, தளவிளைவாக்கப்பட்டே அனுப்பப்பட்டன, அந்த அலைகளை, அதே தளத்தில் உள்ள, சரியான கோணத்திலுள்ள அலைவாங்கிகளாலேயே எடுக்கப்பட்டு, தொலைக்காட்சிப் பெட்டியில் தெளிவாகத் தெரியும், ஆனால், அலைவாங்கியின் தளம் சிறிது மாறியிருந்தாலும், நிகழ்ச்சித் தெளிவாகத் தெரிவதில்லை. ஆகவே, நாம் கூரையின் மேலுள்ள அலைவாங்கியின் கோணத்தை சிறிது மாற்றினாலும் கூட, காட்சியின் தரம் மாறுபடுவதைக் கண்டிருப்போம்.
அதன் அடிப்படைக் காரணம், அலைவாங்கியின் கோணத்தில் ஏற்பட்ட சிறு மாற்றத்தினால், அலைகள் முழுமையாக உள்வாங்கப்படாமல் போவதே! அப்படியானால், அலை அனுப்பப்படுவதும், உள்வாங்கப்படுவதும் அதேத் தளத்தில் இருந்தால் மட்டுமே, அலைமாறுபாடு ஏற்படாமல் தெளிவாக இருக்கும். ஆனால், கொஞ்சமும் சம்பந்தமே இல்லாத இரு வேறு தளங்களில் அனுப்பபடுவதும் வாங்கப்படுவதும் நடந்தால், எப்படியிருக்கும் எனவும் யோசிப்போம்! இதுத் தொலைக்காட்சிப் பெட்டியில் ஒன்றுமேத் தெரியாததற்கு சமம்.
அதே சமயம் இரு வேறு தளங்களில் உள்ள அலைகள், ஒன்றையொன்று ஊடாடி குறுக்கீட்டு விளைவை உண்டு பண்ணுவது என்பதும், சற்றும் பொருந்தாத விடயம். ஆனால் எவ்வளவு பொருந்தாது என்பதைக் கண்டறிய, பஞ்சரத்தினம், விழைந்தார். இதையே, வெவ்வேறு தளவிளைவுற்ற ஒளிக்கதிர்களில் ஒன்றையொன்று மோதச் செய்யும் பொழுது, குறுக்கீட்டு விளைவை ஏற்படுத்தினால் என்ன நடக்கும் என பஞ்சரத்தினம் ஆய்வு செய்தார்.
இதே மாதிரியான வானிலுள்ள, பல்சார் (pulsar) போன்ற தொலைதூர வான்மீன்களிலிருந்து வரும் மின்காந்த அலைகளை வாங்கும் அலைவாங்கிகளின் தளங்களைக் கொண்டு ஆய்வுகளை, சர் சி.வி. இராமனின் புதல்வர், வானியற்பியலாளரான பேராசிரியர் இராதாகிருஷ்ணன் அவர்கள் செய்தார்.
ஒளியியலும் கோள முக்கோணவியலும்
உதாரணத்துக்கு, ஒரு நேரான ஒரு சமதளத்தில் உள்ள முக்கோணம் அல்லது சதுரத்துக்கும், அதுவே ஒரு கோளத்தின் மேல் உள்ள முக்கோணம் அல்லது சதுரத்துக்கும் வித்தியாசம் உள்ளதல்லவா.
பூமியில் ஓரிடத்தில் இருந்து, 500 கிமீ வடக்கு நோக்கிப் போய், அங்கிருந்து இடப்பக்கம் திரும்பி மேற்கு நோக்கிக் கிளம்பி 500 கிமீ போய் மறுபடியும் இடப்பக்கம் திரும்பி 500 கிமீ வந்து, அடுத்தும் 500 கிமீ இடப்பக்கம் திரும்பி வந்தால், நாம் ஆரம்பித்த இடத்திற்கே வந்து விடுவோமா??
இதுவே ஒரு சமதளத்தில் _நடக்கும். ஆனால், பூமியானது கோளவடிவில் ஆனது, ஆகையால், வளைபரப்பின் காரணமாக, தொடர்ந்த இடத்துக்கு வர இன்னும் கொஞ்ச தூரம் பயணிக்கவோ, அல்லது 500 கிமீக்குள் கடந்து விட்டிருக்கவோ வேண்டும்.
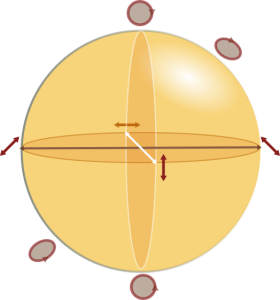
அது சரி, ஏன் திடீரென தளவிளைவில் கோளங்களின் அளவைகள்? ஒரு முப்பரிமாண அல்லது அதிகப்படியான பரிமாணங்கள் உள்ளப் பொருட்களை, எப்படி இரு பரிமாணத் தாளில் வரைகிறோமோ, அதே போல், வெவ்வேறு வகையான தள அதிர்வுகளை, அதன் அதிர்வுகளின் தன்மையான, எந்தத் தளத்தில் அதிர்வுறுகின்றன என்பதைக் கொண்டும், எவ்வளவு செறிவுடன் அதிர்வுறுகின்றன என்பதையும் தாங்கும் சேதிகளை, முப்பரிமாணக் கோளத்தில், பொதியச் செய்யலாம், அவை நம் வசதிக்கேற்பக் குறிப்பதற்கும் கணக்கிடுவதற்கும் பயன்படும் முறையை பிரெஞ்சு இயற்பியலரும் கணிதவியலருமான போன்கெரெ (Henri Poincare) அறிமுகப்படுத்தினார். ஆகையால் அவர் பெயரால், பொன்கெரெ கோளம் என இது அழைக்கப்படுகிறது.
கோளத்தின் நடுப்புள்ளியை, தளவிளைவுறா ஒளியென்றும், கோளத்தின் மேலுள்ளப் புள்ளிகளை தளவிளைவுற்றது என்றும் கூறுவார்கள், அக்கோளத்தின் கோள நடுக்கோட்டில், செங்குத்தாக மற்றும் கிடைமட்டமானத் தளவிளைவைக் குறிக்கும் ஒளியினைக் குறிப்பிடவும், வட, தென் துருவப் புள்ளிகளில் உள்ளவற்றை (வலச் சுற்று, இடச்சுற்று) வட்ட வடிவில் தளவிளைவுற்றது எனவும், ஏனையவை நீள்வட்டத் தளவிளைவுற்ற ஒளியைக் குறிப்பதாகவும் கொள்வோம்.
PoincareSphere3-optics.png ¬
சமதள முக்கோணத்திற்கும் கோளத்தில் அமைந்த முக்கோணத்திற்கும் வேறுபாடு காணுங்கால், ஏற்படும் சிறிய பரப்பு வேறுபாடு பஞ்சரத்தினத்தின் வடிவக் கட்டம் உருவாவதற்கு வழிகோலியது. ஆனால் எவ்வாறு?
வீட்டில் செய்ய இயலும் சில சோதனைகள்:
தளவிளைவாக்கும் படிகங்களைக் கொண்டோ. தளவிளைவாக்கும் ஒளித் தகடுகளைக் கொண்டோ தளவிளைவாக்கலாம். உதாரணத்துக்கு, நீர்மப் படிகத் திரைகள் (Liquid Crystal Displays) தளவிளைவாக்கிய ஒளியை உமிழும் தன்மையுடையவை. தளவிளைவாக்கும் கண்ணாடிகளைப் (Polarized glass) போட்டுக் கொண்டு, நீர்மப் படிகத் திரைகளைப் பார்க்கும் போது, சில கோணங்களில் திரையின் ஒளியின் அளவு அதிகமாகவும், அதையே தலையை சாய்த்துக் காணும் பொழுது,வேறு கோணங்களில் இருளாகவோ அல்லது ஒளியின் செறிவுக் குறைந்தோ இருப்பதைக் காணலாம்.
கீழ்க்காணும் படங்களில் அந்த மாதிரியான சோதனைகள் செய்து காண்பிக்கப்பட்டுள்ளன.
கணினியின் நீர்மப்படிக ஒளித்திரையில் இருந்து வரும் தளவிளைவுற்ற் ஒளி, ஆடியின் வழியாக வரும் பொழுது, வெவ்வேறு கோணங்களில் எப்படி அந்த ஒளிப் பாதிப்படைகிறது என்பதைக் காணலாம்.
IMAG0696.jpg ¬
ஏறத்தாழ செங்குத்தாக ஆடியினைத் திருப்பியதற்கப்புறம் ஒளித் தடைபட்டுள்ளதைக் காண்க.
IMAG0697.jpg ¬
சோதனையினூடே, செலோஃபேன் டேப் எனப்படும் வெளிர் ஒட்டு இழையை இரு மடிப்பாக மடித்து வைக்கும் பொழுது, மேலுள்ளப் படத்தில் மறைக்கப்பட்ட எழுத்துகள் தெரிவதைக் காணலாம், ஏனெனில் ஒட்டு இழை, கணினியில் இருந்து வரும் தளவிளைவாக்கிய ஒளியின் தளத்தினை மாற்றியமைத்துள்ளதைக் காணலாம், இழை வழி வரும் எழுத்துகள் தெளிவாக இருப்பதையும் ஏனைய எழுத்துகள் மறைந்துள்ளதையும் காணலாம்.
IMAG0719.jpg ¬
பற்பல அடுக்குகளினால் ஆன இழைகளைக் கோர்த்து வைக்கும் பொழுது, சீரிலா ஒளிச்சிதறல் இழையில் உள்ளக் கோந்தினாலும், இழையின் மூலக்கூறுவடிவத்தினாலும் ஏற்படுவதால், நிறப்பிரிகை ஏற்படுவதைக் காண்க.
IMAG0717.jpg ¬
IMAG0721.jpg ¬
நம் சோதனை -ஓர் குவாண்டக் கனி!!
நம்முடைய சோதனையும் கூட, பஞ்சரத்தினம் மற்றும் பெரி அவர்கள் சொன்னது போன்றதன், சிறு பிள்ளைகளின் விளையாட்டுப் போன்றதன் ஒரு சோதனைவடிவமே, ஆயினும் சிறப்பாக ஒரு இயற்பியல் சோதனை நடந்திருக்கிறது!
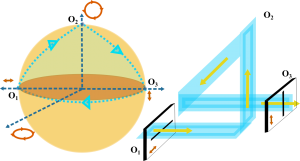
நம் 500 கிமீ பயண எடுத்துக்காட்டில், குறைந்தது, ஓரிடத்தில் ஆரம்பித்து, 3 இடங்களைக் கடந்து, ஆரம்பித்த இடத்துக்கு வருவதைப் பார்த்தோம் அல்லவா, அதே போல், நாம் தளவிளைவான மூன்று ஒளிக்கதிர்களை (ஒ1, ஒ2, ஒ3) வெவ்வேறு தளவிளைவாக்கியைக் கொண்டு உருவாக்கவேண்டியது, பின் இவற்றை ஒன்றன்மீது ஒன்றாகப் (ஒ1 மீது ஒ2, ஒ2 மீது ஒ3, ஒ3 மீது ஒ1) பாய்ச்சும் பொழுது, அலைப் பண்பால், இந்த மூன்றுக் கதிர்களும், அவ்வவற்றின் அகடு முகடுகள் கூடுவதால், வெளிச்சம் மற்றும் இருட்கோடுகளை உருவாக்கும், ஒளிக்கதிர்கள் வெவ்வேறுக் கட்டங்களில் கூடுவதால் உண்டாவது இது. ஆயினும், இந்தக் கதிர்களின் அதிர்வுகள், வெவ்வேறு தளங்களில் இருந்தால், அகடு முகடுகள் கூடாமல், அப்படியே இருக்கவேண்டும்,ஆயினும் குறுக்கீட்டு விளைவை உண்டு பண்ணுகின்றன.
PoincareSphere-Optics-TriangularPath.png ¬
ஒ1 எனப்படுவதைக் கணினியில் இருந்து வரும் ஒளியாகவும் கண்ணாடி ஒட்டு இழையில் பட்டு வரும் ஒளியை ஒ2 ஆகவும், போலரைஸ்டு கண்ணாடியில் இருந்து ஒளியை ஒ3 எனவும் கொள்வோம். ஒ3 பகுப்பானாய் உள்ள போது ஒ1 எனப்படும் கணினி ஒளியைத் தடுத்து மறைக்கிறது. அப்படியெனில் ஒ1 கணினி ஒளியின் தளமும் கண்ணாடியின் தளமும் நேர்எதிர் ஆனவை. ஆனால், ஒட்டு இழை வழியாக வரும் பொழுது, கணினி ஒளியின் தளம் மாற்றப்பட்டுக் கண்ணாடி வழியாகத் தெரியச் செய்கிறது.
இம்மூன்று ஒளிக்கற்றைகளையும் வெவ்வேறுப் புள்ளிகளில், அந்தந்த ஒளியின் தளங்களைப் பொறுத்து, போன்கெரெ கோளத்தில் குறிப்பிடலாம் அல்லவா, அவற்றை இணைக்கும் பொழுது, கோளத்தில் முக்கோணம் உருவாவதைக் காணலாம், அந்தக் கோளப் பரப்பு வேறுபாடானது, கணக்கிடும் பொழுது அந்த ஒளி-இருள் பட்டைகளின் காரணமாவதுத் தெரிந்தது. இந்த பரப்பு வேறுபாடு, கோளத்தில் மையப்புள்ளியில் இருந்து இப்புள்ளிகளால் உருவானத் திண்மம் (ஆப்பு தனைப் போன்ற ஒரு வடிவம்) உண்டாக்கும் கோணத்தின் நேர் விகிதத்தில் இருப்பதையும் உணர முடிந்தது.
கணினி, இழை, கண்ணாடி ஆகியனவற்றின் தளங்களை சரியாகக் கணிக்கும் பட்சத்தில் பஞ்சரத்தினத்தின் வடிவக்கட்டத்தைக் கணக்கிடலாம். இதில் கடைசியாக நாம் காணும் ஒளி, பஞ்சரத்தினத்தின் வடிவக்கட்டத்தைத் தாங்கியே வருகிறது! இதை இன்னும் சனரஞ்சகமாகக் கூறினால், குவாண்டக் கணினிக்குத் தேவையான ஒரு முக்கியமானக் கருவியை நாம் இலகுவாக செய்திருக்கிறோம்!
நவீன பயன்பாடு
இதை பஞ்சரத்தினம் அவர்கள் கண்டறிந்து, பற்பல வருடங்கள் கழித்து, குவாண்ட இயற்பியலில் ஒரு குவாண்டத்துகளின் சுழற்சிப் (spin) பண்பானது, இதே “மாதிரியான” கட்ட வேறுபாட்டினைத் தாங்கி வந்ததை மைக்கேல் பெரி அவர்கள் கண்டறிந்து பிரசுரித்தார், அதைத் தொடர்ந்து, பஞ்சரத்தினத்தின் ஆய்வுகள், பேராசிரியர்கள் இராமசேஷன், இராஜாராம் நித்யானந்தா மூலம் தக்க சமயத்தில் வெளிக்கொணரப்பட்டது.
பின்பு இந்திய அறிவியற்கழக, இராமன் ஆய்வுக்கழக மற்றும் கணித அறிவியற்கழகப் பேராசிரியர்களான முகுந்தா, ஜோசப் சாமுவேல், இராஜேந்திர பண்டாரி, சைமன் ஆகியோரால் பஞ்சரத்தினத்தின் மற்றும் பெரியின் வடிவியற்கட்டம் அமையும் விதங்களை, குவாண்ட புலங்களிலும், இயக்கவியலிலும், குவாண்ட ஒளியியலைக் குலங்கள் வழிக் காண்பதிலும் (Group theoretical approach to quantum optics) என வெவ்வேறு அமைவுகளில் கண்டறிந்தனர்.
இப்படி வெவ்வேறு அளவுகளில் நடந்த கோட்பாட்டுரீதியான, அதே அளவில் சோதனை அடிப்படையிலான ஆய்வுகளின் விளைவு, வடிவக் கட்டங்களின் பயன்பாடும் அதன் மூலமும் ஆழ்ந்த தத்துவார்த்த இயற்பியலில் முக்கியமான விசயங்களை உணர்த்துவதோடு, நவீன அறிவியலின் பரிணாமத்தால், பயன்பாட்டு அளவிலும் பயன்படுத்த முடியும் என ஆய்வு செய்கின்றனர்.
தற்காலத்தில், குவாண்டக் கணினிகளை, குவாண்டச் சுற்றுகளால் (circuits) வடிவமைக்கும் பொழுது, இதே மாதிரியான தளவிளைவாக்கிகளின் அடிப்படையைக் கொண்டு செய்ய முடியும், ஆனால், குவாண்டக் கணிணிகள், பெரும்பாலும், குவாண்ட ஒளியின் பண்புகள், அணுக்கரு, அணு, எதிர்மின் துகள்கள், அல்லது நியூட்ரினோ போன்ற மீச்சிறுதுகள்களாலும் உருவாக்கப் பரிந்துரைகள் செய்யப்படுகிறது. இவை எல்லாம், சூழலின் வெப்பம், மற்றும் வெவ்வேறு வகையான இயற்கை காரணிகளால் மிக எளிதாகப் பாதிக்கப்படும், இதனால், குவாண்ட கணினியில் உள்ள விவரங்கள், மிகச் சிறிய நேரத்திற்கு மட்டுமே சேமித்து வைக்கப்பட முடியும்.
அந்த மீச்சிறு நேரத்திலும், இன்னபிற வேண்டாத விளைவுகளை உண்டு பண்ணும் குவாண்ட செயல்பாடுகளால், கணக்கீட்டில் தவறுகள் நேரலாம். அந்த செயல்பாடுகளை, பஞ்சரத்தின வடிவக்கட்டத்தைக் கொண்டு உருவாக்கும் செயலிகளைக் கொண்டு தவறு நேராமல் செய்யலாம். நாம் ஏற்கனவேப் பார்த்ததில் பான்கெரெ கோளத்தில் உண்டாகும் திண்மத்தின் கன அளவானது, ஆற்றல் மாறாவிதி போன்ற அடிப்படை விசயங்களால்,பாதுகாக்கப்படுவதால், பிழைகள் நேருவதுத் தடுக்கபடுவதாக கருதுகோள் கோரப்படுகிறது. முன்காலங்கள் போல் இல்லாமல், தற்பொழுது வளர்ந்து வரும் பொருண்மை அறிவியலின் (Material science) வளர்ச்சியில், இம்மாதிரியானக் குவாண்ட செய்தி பரிமாற்றத்துக்கும் கணக்கீட்டுக்கும் தேவையானப் பொருண்மங்க_ளை உருவாக்கிக் கொண்டே வருகிறார்கள். இதனால், பஞ்சரத்தினத்தின் வடிவியற்கட்டம் சார்ந்த விசயங்களை வரும் வருடங்களில் குவாண்ட கணினிகளிலும் பயன்படுத்தலாம்.
பஞ்சரத்தினத்தைத் தொடர்ந்து பெரி வடிவக் கட்டமும், அதைத் தொடர்ந்து அஹரனோவ் – ஜீவா ஆனந்தன் (இலங்கை தமிழ் இயற்பியலாளர்) வடிவக் கட்டமும், தவிர, இடவியல் கோட்பாட்டின் பலக் கூறுகளை இயற்பியலின் கட்டுமானத்தைக் கொண்டுத் தெளிவுறுத்தவும் இக்கோட்பாடுகள் உதவிகரமாய் உள்ளன.
60 வருடங்கள் கழித்து, மீண்டும் பஞ்சரத்தினத்தின் ஆய்வு மிகப் பெரியத் தாக்கத்தினை செய்து கொண்டிருக்கிறது. மிகக் குறுகியக் காலமே (35 வயது) வாழ்ந்து மறைந்த பஞ்சரத்தினம் அறிவியற் துறையில் மட்டுமல்லாது, மிக விரிவான சமுதாயப் பார்வையும் சமூக மேம்பாடு குறித்தத் தெளிவினையும் கொண்டிருந்ததோடு மட்டுமல்லாமல், அதற்கான வேலைகளில் ஈடுபட்டதால் உண்டான நோய்த் தொற்று, அவரின் இளமைக் கால இறப்புக்குக் காரணமானது.
ஆயினும் ஶ்ரீனிவாச இராமானுஜன், இராமன் போன்றோரின் ஆய்வின் தாக்கம் போல் பஞ்சரத்தினத்தின் தாக்கமும் இயற்பியலில் இன்றளவிலும் அளப்பரியதாக உள்ளதைக் காண முடிகிறது.
உசாவி
அறிவியல்சார்/சாராக் கட்டுரைகள்:
[1] Rajaram Nityananda, Resonance, Vol. 18, Issue 4. page. 301 — 305 (2013)
S Pancharatnam (1934–1969): Three Phases
Kausalya Ramaseshan, ibid.
NV Madhusudana, ibid.
GW Series, ibid.
http://www.ias.ac.in/resonance/Volumes/18/04/0301-0305.pdf
[2] Current science special issue on Pancharatnam, Vol.67, Issue. 4 (1994)
அறிவியற்கட்டுரைகள்
[3] S. PANCHARATNAM, Proc. Indian Acad. Sci. 45, 402 (n.d.).
[4] S. PANCHARATNAM, Proc. Indian Natl. Sci. Acad., A 44, 247 (1956).
[5] S. PANCHARATNAM, Proc. Indian Natl. Sci. Acad., A 46, 1 (1957).
[6] S. PANCHARATNAM, Proc. Indian Natl. Sci. Acad., A 44, 398 (1956).
[7] M. V. Berry, Proc. R. Soc. London. A. Math. Phys. Sci. 392, 45 (1984).
——
______________________________
Nageswaran Rajendran
Experimentelle Physik III
Fachbereich Physik
Technische Universitaet Dortmund
D-44221 Dortmund
Germany
http://chaos.physik.tu-
- ஈராக்கில் உண்மை அறியும் குழுவும், அதன் முடிவுகளும்
- வானம்பாடிகளும் ஞானியும்
- உள்ளிருந்து உடைப்பவன்
- பாவப்பட்ட ஜென்மங்களின் கதை [ உதயகண்ணனின் ’இருவாட்சி’ வெளியீடாக வர இருக்கும் நாவல் குமாரகேசனின் “அரபிக்கடலோரத்தில்” நாவலுக்கான அணிந்துரை ]]’
- சுந்தரி காண்டம் 5. அபிராமி அற்புத சுந்தரி
- பஞ்சரத்தினத்தின் வடிவியற்கட்டம் (Pancharatnam geometric phase) தளவிளைவுற்ற ஒளியும் நவீன குவாண்டத் தொடர்பு அறிவியலும்
- BLOSSOMS FROM THE BUDDHA – THE DHAMMAPADA, (The Buddha’s path of wisdom) RETOLD IN RHYMING VERSES
- குப்பி
- நாக்குள் உறையும் தீ
- கண்டெடுத்த மோதிரம்
- தினம் என் பயணங்கள் -45 இலக்கை நோக்கிய பயணம்!
- ஸ்ரீரங்கம் சௌரிராஜன் எழுதிய ‘ கவிதையும் என் பார்வையும் ‘ —– ஒரு பார்வை
- திரு. ஈரோடு. கதிர் அவர்களின் கட்டுரைத் தொகுப்பு, கிளையிலிருந்து வேர் வரை – திறனாய்வு
- நிழல்களின் நீட்சி
- வரும் 11-10-2015 ஞாயிறு “வலைப்பதிவர் திருவிழா-2015” காலை 9.00 முதல் மாலை 5.00 வரை ஆரோக்கிய மாதா மக்கள் மன்றம், பீவெல் மருத்துவமனைஎதிரில், ஆலங்குடிச் சாலை, புதுக்கோட்டை
- பொன்னியின் செல்வன் படக்கதை 4
- தொடுவானம் 85. புதிய பூம்புகார்
- அன்பாதவன் கவிதைகள் – ஒரு பார்வை
- சைனா 2020 ஆண்டுக்குள் முதன்முறையாக நிலவின் மறுபுறத்தில் தளவுளவியை இறக்கத் திட்டமிடுகிறது.
- யட்சன் – திரை விமர்சனம்
- அவன், அவள், அது…!? (முதல் அத்தியாயம் )
- நெஞ்சு வலி
- அறிவியல் கதிர் நிலத்தடிநீர் வளத்தைப் புதுப்பிக்க மழைநீர் சேகரிப்பு ஒன்றே வழி
- X-குறியீடு